
Tudo come�ou no s�culo 16 com o famoso explorador ou pirata (dependendo do seu ponto de vista) Walter Raleigh. Mas ele n�o era matem�tico nem, pelo que sabemos, tinha problemas com beijos.
O que ele tinha eram balas de canh�o e uma pergunta: qual era a maneira mais eficaz de empilh�-las para minimizar ao m�ximo o espa�o que ocupavam em suas embarca��es?
A quest�o de Raleigh geraria um mist�rio matem�tico que povoaria mentes brilhantes por centenas de anos.
Ele fez a pergunta a seu consultor cient�fico em uma viagem � Am�rica em 1585, o ilustre matem�tico Thomas Harriot, que deu a ele uma solu��o: a melhor maneira de armazenar suas balas de canh�o era organiz�-las em forma de pir�mide.
Em um manuscrito de 1591, Harriot fez para ele uma tabela mostrando como, dado o n�mero de balas de canh�o, algu�m poderia calcular quantas colocar na base de uma pir�mide com uma base triangular, quadrada ou oblonga (alongada).
Leia tamb�m: O �nico restaurante do mundo que serve carne cultivada em laborat�rio
Mas Harriot continuou pensando sobre o assunto, e levou em considera��o as implica��es para a teoria at�mica da mat�ria, que estava em voga na �poca.

Ao comentar sobre essa teoria em correspond�ncia com o amigo Johannes Kepler, o famoso astr�nomo, ele mencionou o problema do armazenamento.
Kepler sup�s que a maneira ideal de minimizar o espa�o deixado pelas lacunas entre as esferas era fazer com que os centros das esferas em cada camada ficassem acima de onde as esferas da parte de baixo se "beijavam".
Isso � o que muitas vezes se faz com as frutas nos mercados, por exemplo.
Essa forma, que parece t�o intuitivamente �bvia, se revelou extremamente dif�cil de provar matematicamente.
Embora muitos tenham tentado, incluindo Johann Carl Friedrich Gauss, "o pr�ncipe da matem�tica", a mesma s� foi comprovada quase quatro s�culos depois, em 1998, com o trabalho de Thomas Hales, da Universidade de Michigan, nos EUA, e o poder de um computador.
E nem sequer essa verifica��o convenceu todos os matem�ticos; ainda hoje h� quem n�o a considere digna da conjectura de Kepler - que indica que se empilhamos esferas iguais, a densidade m�xima � alcan�ada com um empilhamento piramidal de faces centradas.
As inc�gnitas das esferas
Essa n�o foi a �nica dor de cabe�a causada por objetos esf�ricos.
Na verdade, uma ampla categoria de problemas matem�ticos � chamada de "problemas de empacotamento de esferas".
Resolv�-los serviu para desde explorar a estrutura dos cristais at� otimizar os sinais enviados por celulares, sondas espaciais e internet.
E assim como Raleigh com suas balas de canh�o, as ind�strias de log�stica, de mat�rias-primas e muitas outras dependem fortemente de m�todos de otimiza��o fornecidos pela matem�tica.
Matem�ticos descobriram, por exemplo, que esferas empilhadas aleatoriamente tendem a ocupar qualquer espa�o com uma densidade de aproximadamente 64%. Mas se voc� coloc�-las cuidadosamente em ordem de maneiras espec�ficas, poder� chegar a 74%.

Esses 10% representam uma economia n�o apenas nos custos de transporte, mas tamb�m nos danos ao meio ambiente.
Mas aplica��es pr�ticas como essa requerem provas matem�ticas, e o empacotamento de esferas trouxe inc�gnitas particularmente dif�ceis, assim como a conjectura de Kepler.
Uma delas surgiu de uma conversa entre Isaac Newton, um dos maiores cientistas de todos os tempos, e David Gregory, o primeiro professor universit�rio a ensinar as teorias de ponta de Newton.
Era um problema de n�mero de "beijos", mas...
O que s�o?
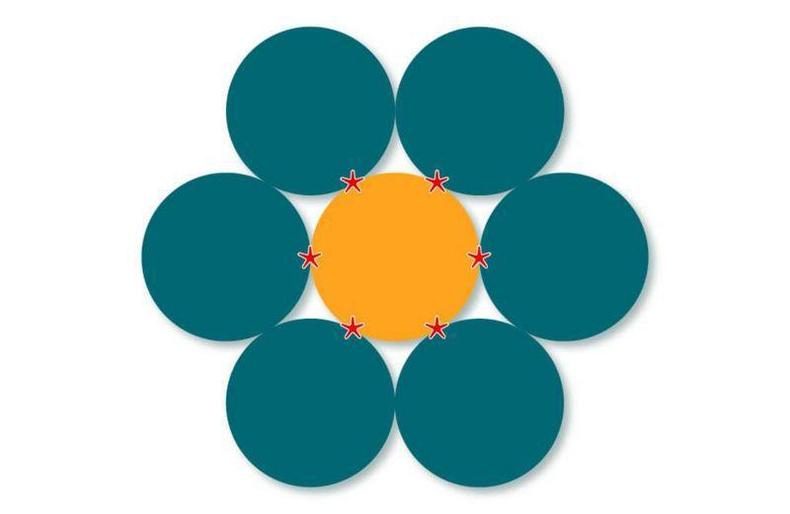
Imagine que voc� tem v�rios c�rculos de papel�o do mesmo tamanho e deseja col�-los em um quadro ao redor de um deles.
O n�mero de "beijos" � igual ao n�mero m�ximo de c�rculos que voc� consegue colocar "beijando" - ou tocando - o central.
Simples assim.
Acontece que os matem�ticos mostraram que no m�ximo 6 c�rculos podem ser colocados em torno do inicial, ent�o o n�mero de "beijos" � 6.
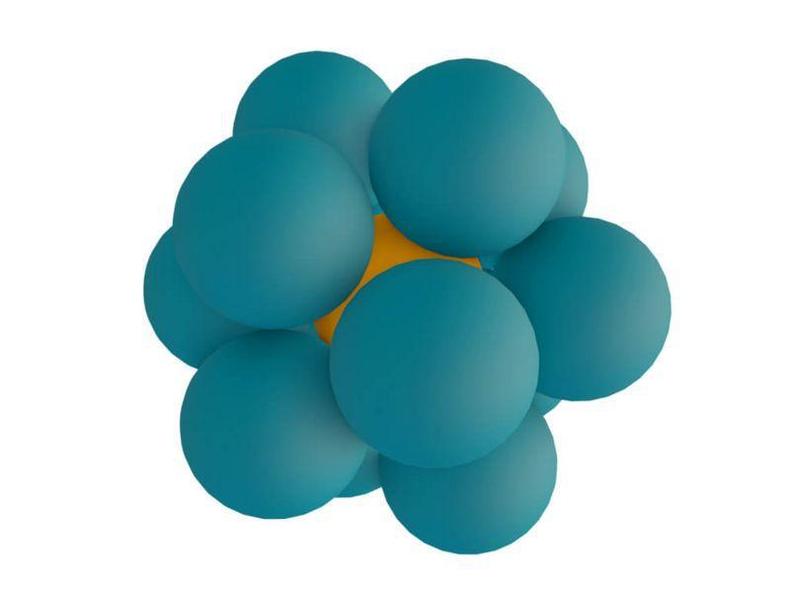
Agora imagine que em vez de c�rculos de papel�o, voc� tem bolas de borracha, todas do mesmo tamanho.
Novamente a pergunta �: qual � o n�mero m�ximo de bolas que voc� pode colocar ao redor de uma no centro?
Ao adicionar essa terceira dimens�o - o volume -, a quest�o de especificar o n�mero de "beijos" se tornou mais complicada.
E foram necess�rios dois s�culos e meio para descomplic�-la.
Newton e Gregory
A quest�o come�ou com aquela famosa discuss�o entre Newton e Gregory, ocorrida em 1694 no campus da Universidade de Cambridge, no Reino Unido.
Newton j� tinha 51 anos, e Gregory fez uma visita de v�rios dias, durante a qual conversaram sem parar sobre ci�ncia.
A conversa foi bastante unilateral, com Gregory anotando tudo o que o grande professor dizia.
Um dos pontos discutidos e registrados no memorando de Gregory foi quantos planetas giram em torno do Sol.
A partir da�, a discuss�o saiu pela tangente, para a quest�o de quantas esferas do mesmo tamanho podem ser dispostas em camadas conc�ntricas de modo que toquem uma central.
Gregory afirmou - sem muitos pre�mbulos - que a primeira camada em torno de uma bola central tinha no m�ximo 13 esferas.
Para Newton, o n�mero de "beijos" seria 12.
Gregory e Newton nunca chegaram a um acordo e nunca souberam qual era a resposta certa.
Hoje em dia, o fato de que o maior n�mero de esferas que pode "beijar" uma central � comumente chamado de "n�mero de Newton" revela quem estava certo.
O debate s� parou em 1953, quando o matem�tico alem�o Kurt Sch�tte e o holand�s B. L. van der Waerden mostraram que o n�mero de "beijos" em tr�s dimens�es era 12 - e apenas 12.
A quest�o era importante porque um grupo de esferas empacotadas ter� um n�mero m�dio de "beijos", o que ajuda a descrever matematicamente a situa��o.
Mas h� quest�es n�o resolvidas.
Milhares de beijos
Al�m das dimens�es 1 (intervalos), 2 (c�rculos) e 3 (esferas), o problema do "beijo" est� quase sem resolu��o.
H� apenas dois outros casos em que esse n�mero de "beijos" � conhecido.
Em 2016, a matem�tica ucraniana Maryna Viazovska estabeleceu que o n�mero de beijos na dimens�o 8 � 240, e na dimens�o 24 � 196.560.
Para as outras dimens�es, os matem�ticos foram reduzindo lentamente as possibilidades a faixas estreitas.
Para dimens�es maiores que 24, ou uma teoria geral, o problema est� em aberto.
H� v�rios obst�culos para uma solu��o completa, incluindo limita��es computacionais, mas a expectativa � de que haja um avan�o importante nesse problema nos pr�ximos anos.
De que adianta, no entanto, empacotar esferas de dimens�o 8, por exemplo?
O top�logo alg�brico Jaume Aguad� respondeu a essa pergunta em um artigo de 1991 intitulado "Cem anos de E8".
"� usado para fazer chamadas telef�nicas, ouvir Mozart em um CD, enviar um fax, assistir � televis�o via sat�lite, conectar-se, por meio de um modem, a uma rede de computadores."
"Serve para todos os processos em que � necess�ria a transmiss�o eficiente de informa��es digitais."
"A teoria da informa��o nos ensina que os c�digos de transmiss�o de sinais s�o mais confi�veis %u200B%u200Bem dimens�es maiores, e o ret�culo de E8, com sua simetria surpreendente e dada a exist�ncia de um decodificador apropriado, � uma ferramenta fundamental na teoria de codifica��o e transmiss�o de sinais."
- Este texto foi publicado em https://www.bbc.com/portuguese/articles/cxe5j1yg4llo
/imgs.em.com.br/bbc/bbcnews.jpg)